ALL ABOUT MATHEMATICS
Sunday, 12 June 2016
INTRODUCTION PROBABLITY
WHAT IS PROBABILITY???
Probability is the measure of the likelihood that an event will occur. Probability is quantified as a number between 0 and 1 (where 0 indicates impossibility and 1 indicates certainty).The higher the probability of an event, the more certain we are that the event will occur. A simple example is the tossing of a fair (unbiased) coin. Since the coin is unbiased, the two outcomes ("head" and "tail") are equally probable; the probability of "head" equals the probability of "tail." Since no other outcome is possible, the probability is 1/2 (or 50%) of either "head" or "tail". In other words, the probability of "head" is 1 out of 2 outcomes and the probability of "tail" is also, 1 out of 2 outcomes, expressed as 0.5 using the above mentioned quantification system.
Friday, 10 June 2016
Thursday, 9 June 2016
Algebra
Introduction of Algebra
Algebra is one of the broad parts of mathematics, together with number theory, geometry and analysis. In its most general form, algebra is the study of mathematical symbols and the rules for manipulating these symbols it is a unifying thread of almost all of mathematics.
ALGEBRA EXAMPLE
Solving an equation:
Why Use a Letter?
| Because: | |
| it is easier to write "x" than drawing empty boxes (and easier to say "x" than "the empty box"). | |
| if there are several empty boxes (several "unknowns") we can use a different letter for each one. |
So x is simply better than having an empty box. We aren't trying to make words with it!
And it doesn't have to be x, it could be y or w ... or any letter or symbol we like.
How to Solve
Algebra is just like a puzzle where we start with something like "x − 2 = 4" and we want to end up with something like "x = 6".
But instead of saying "obviously x=6", use this neat step-by-step approach:
- Work out what to remove to get "x = ..."
- Remove it by doing the opposite (adding is the opposite of subtracting)
- Do that to both sides
Here is an example:
| We want to remove the "-2" | To remove it, do the opposite, in this case add 2: | Do it to both sides: | Which is ... | Solved! |
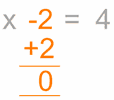 | 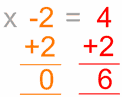 |
Wednesday, 8 June 2016
Tuesday, 7 June 2016
Introduction to Quadratic Equations.
Definition of a quadratic equation
A quadratic equation in x is an equation that can
be written in the
form
2 0, , ,
0.
ax bx c where a b and c are
real numbers with a
+ +=
≠
A quadratic equation in x also called a second degree
polynomial equation in x.
Quadratic formula and its derivation
Completing the square can be used to derive a general formula for solving quadratic equations, called the quadratic formula.[5] The mathematical proof will now be briefly summarized.[6] It can easily be seen, by polynomial expansion, that the following equation is equivalent to the quadratic equation:
Taking the square root of both sides, and isolating x, gives:
Some sources, particularly older ones, use alternative parameterizations of the quadratic equation such as ax2 + 2bx + c = 0 or ax2 − 2bx + c = 0 ,[7] where b has a magnitude one half of the more common one, possibly with opposite sign. These result in slightly different forms for the solution, but are otherwise equivalent.
A number of alternative derivations can be found in the literature. These proofs are simpler than the standard completing the square method, represent interesting applications of other frequently used techniques in algebra, or offer insight into other areas of mathematics.
A lesser known quadratic formula, as used in Muller's method, and which can be found from Vieta's formulas, provides the same roots via the equation:
One property of this form is that it yields one valid root when a = 0, while the other root contains division by zero, because when a = 0, the quadratic equation becomes a linear equation, which has one root. By contrast, in this case the more common formula has division by zero in both cases.
Monday, 6 June 2016
Subscribe to:
Comments (Atom)


